Math challenge!
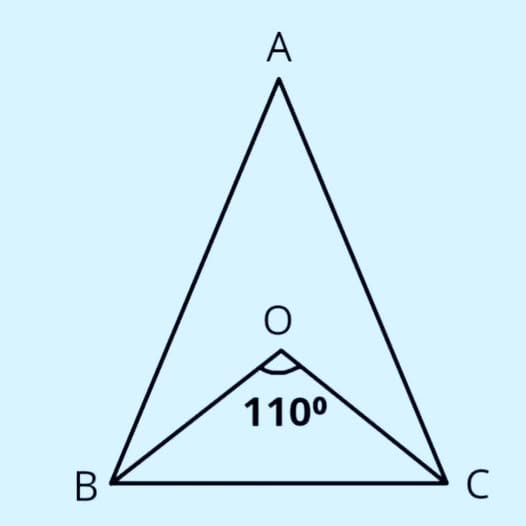
When I have some free time, I hope to post some daily math challenges for kids visiting the blog. I'll start it off with some easy ones today and then get harder and harder!

Answer
Oh come on, you know this! Super easy pattern, increases by 5, by 10, by 15, by 20! Answer is 60!
Answer
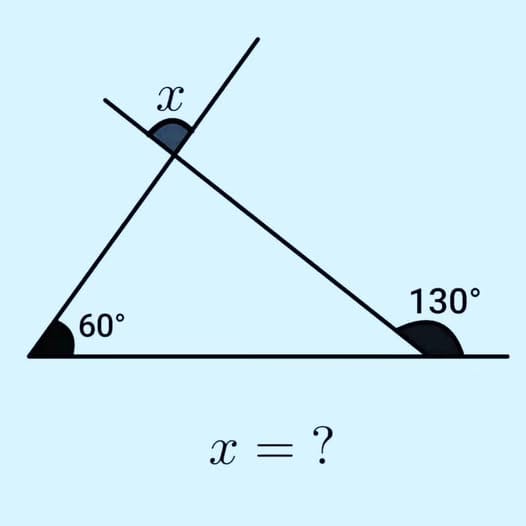
Finding Angle X: Exterior Angles and Triangles
This problem involves finding an exterior angle of a triangle. It beautifully demonstrates one of the most useful theorems in geometry: the Exterior Angle Theorem. Let's work through it step by step!
Given Information
Let's identify what we see:
- A triangle with vertices at the bottom left, bottom right, and top
- An angle of 60° at the bottom left vertex (interior angle)
- An angle of 130° at the bottom right vertex (this is an exterior angle)
- An angle x at the top vertex (this is also an exterior angle)
- We need to find: x = ?
Step 1: Understanding Interior vs. Exterior Angles
Interior Angles: The angles inside the triangle
Exterior Angles: Formed when we extend one side of the triangle beyond a vertex
At the bottom right corner:
- The exterior angle is 130° (shown in the diagram)
- The interior angle and exterior angle form a linear pair (they're supplementary)
- Interior angle + Exterior angle = 180°
Let's find the interior angle at the bottom right:
Interior angle = 180° - 130° = 50°
Step 2: Finding All Interior Angles
Now we know two interior angles of the triangle:
- Bottom left: 60°
- Bottom right: 50°
- Top: ?
Using the Triangle Angle Sum Property (all interior angles sum to 180°):
60° + 50° + Top angle = 180°
110° + Top angle = 180°
Top angle = 70°
So the interior angle at the top vertex is 70°.
Step 3: Finding Exterior Angle x
The angle x is an exterior angle at the top vertex. Since the interior angle at the top is 70°, and interior and exterior angles at the same vertex form a linear pair:
Interior angle + x = 180°
70° + x = 180°
x = 110°
Method 2: The Exterior Angle Theorem (Shortcut!)
There's a faster way to solve this using the Exterior Angle Theorem:
Exterior Angle Theorem: An exterior angle of a triangle equals the sum of the two non-adjacent (remote) interior angles.
For angle x:
- The two non-adjacent interior angles are 60° and 50°
- Therefore: x = 60° + 50° = 110°
This gives us the same answer instantly!
The Answer
x = 110°
Why the Exterior Angle Theorem Works
Let's prove why this theorem is true:
- Let the three interior angles be A, B, and C
- We know: A + B + C = 180° (angle sum property)
- An exterior angle at vertex C is supplementary to C
- Exterior angle = 180° - C
- Substituting C = 180° - A - B:
- Exterior angle = 180° - (180° - A - B)
- Exterior angle = 180° - 180° + A + B
- Exterior angle = A + B ✓
This proves that an exterior angle equals the sum of the two remote interior angles!
Verification
Let's check our answer using both methods:
Method 1 (Linear Pair):
- Interior angle at top = 70°
- x = 180° - 70° = 110° ✓
Method 2 (Exterior Angle Theorem):
- x = 60° + 50° = 110° ✓
Complete Triangle Check:
- Interior angles: 60° + 50° + 70° = 180° ✓
- Exterior angle at bottom right: 180° - 50° = 130° ✓
- Exterior angle at top: 180° - 70° = 110° ✓
Everything checks out!
Key Concepts to Remember
Triangle Angle Sum Property:
- The sum of all interior angles in a triangle is always 180°
Linear Pair:
- Two angles that form a straight line are supplementary (sum to 180°)
- Interior and exterior angles at the same vertex form a linear pair
Exterior Angle Theorem:
- An exterior angle of a triangle equals the sum of the two remote interior angles
- This is one of the most useful shortcuts in geometry!
Problem-Solving Strategies
When you see an exterior angle problem, you have two approaches:
Approach 1 (Step-by-Step):
- Find all interior angles using the triangle angle sum property
- Use the linear pair property to find the exterior angle
Approach 2 (Direct):
- Use the Exterior Angle Theorem immediately
- Add the two remote interior angles
Both work, but the Exterior Angle Theorem is faster!
Practice Problems
Try these similar problems:
Problem 1: If a triangle has interior angles of 45° and 70°, what is the exterior angle at the third vertex?
- Answer: 45° + 70° = 115°
Problem 2: If an exterior angle is 145° and one remote interior angle is 85°, what is the other remote interior angle?
- Answer: 145° - 85° = 60°
Problem 3: Can an exterior angle of a triangle ever be smaller than one of its interior angles?
- Answer: No! An exterior angle is always greater than either remote interior angle (since it equals their sum).
Real-World Applications
The Exterior Angle Theorem appears in:
- Architecture: Calculating roof angles and supports
- Navigation: Determining angles when changing direction
- Engineering: Analyzing truss structures and frameworks
- Computer Graphics: Rendering 3D objects and calculating viewing angles
The Exterior Angle Theorem is a powerful tool that can save you time on many geometry problems. Master it, and you'll breeze through triangle problems!
Answer
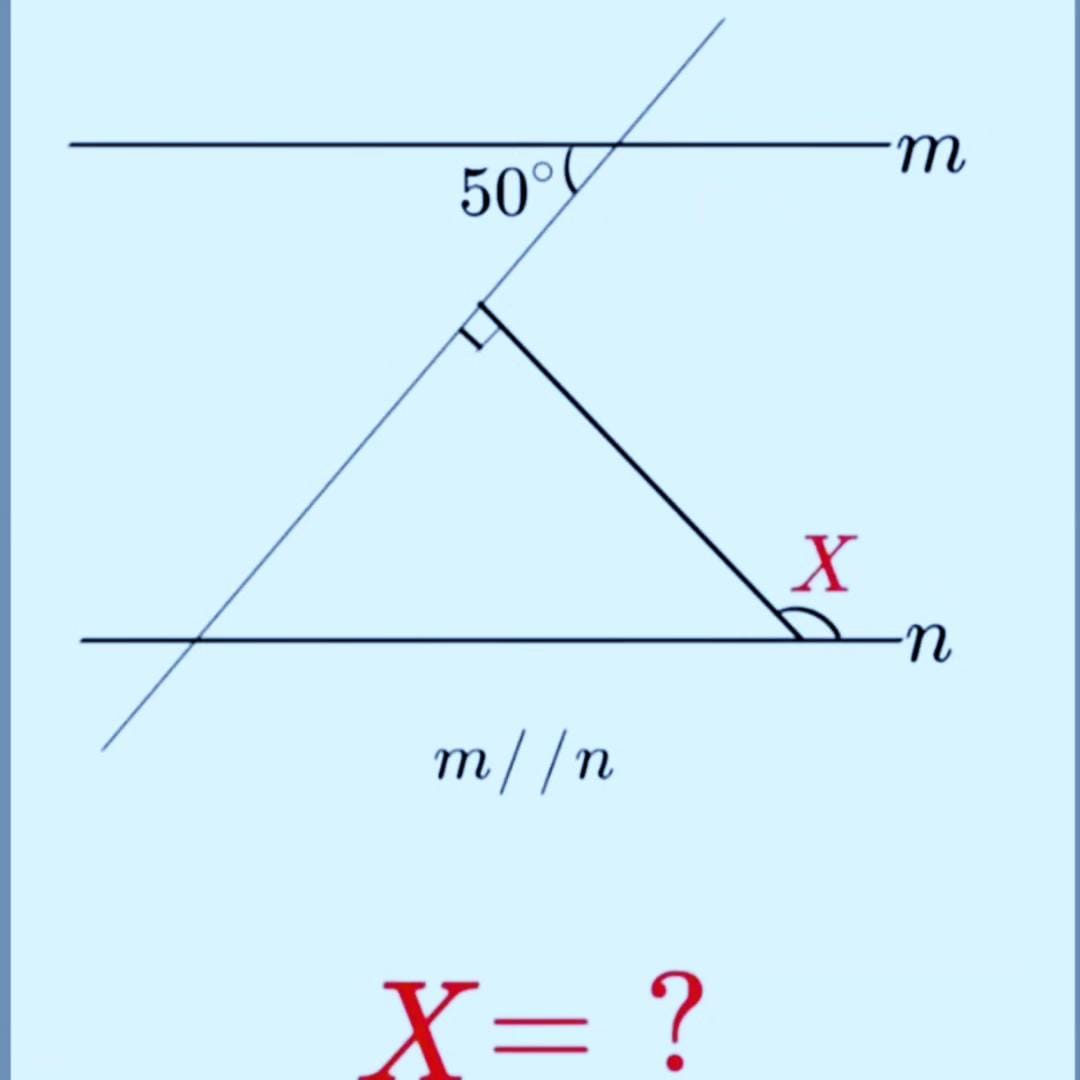
Finding Angle X: Parallel Lines and Triangles
In this problem, we need to find the value of angle x in a triangle formed between two parallel lines. The key to solving this is understanding how parallel lines interact with transversals and applying the angle sum property of triangles.
Given Information
Let's identify what we know:
- Lines m and n are parallel (indicated by m // n)
- A transversal line crosses both parallel lines
- The angle between the transversal and line m is 50°
- A right triangle is formed with:
- One vertex on the transversal with a 90° angle (marked with a square)
- Its base lying on line n
- Angle x at the bottom right corner
- We need to find: x = ?
Step 1: Understanding Parallel Lines and Transversals
When a transversal crosses two parallel lines, it creates several important angle relationships:
Key Angle Relationships:
- Corresponding Angles are equal
- Alternate Interior Angles are equal
- Co-interior Angles are supplementary (add up to 180°)
In our problem:
- The transversal makes a 50° angle with line m (shown at the top)
- Since m // n, the transversal will make related angles with line n
Step 2: Finding the Angle at Line n
The 50° angle shown is the acute angle between the transversal and line m (on the upper side).
When we look at where the transversal crosses line n, we need to find the alternate interior angle.
Alternate Interior Angles Theorem: When a transversal crosses parallel lines, alternate interior angles are equal.
The angle that the transversal makes with line n (on the left side of the triangle) is the alternate interior angle to the 50° angle at line m.
Therefore, this angle is also 50°.
Step 3: Identifying the Triangle's Angles
Now let's label all three angles of our triangle:
- Top angle = 90° (the right angle marked with a square)
- Bottom left angle = 50° (the angle between the transversal and line n)
- Bottom right angle = x (what we're looking for)
Step 4: Using the Angle Sum Property
One of the fundamental properties of triangles is:
The sum of all interior angles in a triangle equals 180°
So we can write:
90° + 50° + x = 180°
Step 5: Solving for x
Now it's just simple algebra:
90° + 50° + x = 180°
140° + x = 180°
x = 180° - 140°
x = 40°
The Answer
x = 40°
Why This Works: The Complete Picture
Let's verify our answer makes sense:
- Parallel Lines: The 50° angle at line m creates a 50° alternate interior angle at line n ✓
- Right Triangle: We have a 90° angle at the top ✓
- Angle Sum: 90° + 50° + 40° = 180° ✓
This problem beautifully demonstrates how properties of parallel lines combine with properties of triangles. The key insight was recognizing that:
- Parallel lines preserve angles through their relationship with the transversal
- The triangle's angles must sum to 180°
- These two facts together allow us to find the missing angle
Key Concepts to Remember
Parallel Lines Cut by a Transversal:
- Alternate interior angles are equal
- Corresponding angles are equal
- These relationships are crucial for solving problems involving parallel lines
Triangle Angle Sum:
- All triangles have interior angles that sum to 180°
- If you know two angles, you can always find the third
Problem-Solving Strategy:
- Identify what geometric properties apply (parallel lines, triangles, etc.)
- Use angle relationships from parallel lines to find unknown angles
- Apply the triangle angle sum property
- Solve algebraically
Practice Problem
Try this similar problem:
- If the angle at line m was 65° instead of 50°, what would x be?
- Answer: x would be 25° (since 90° + 65° + 25° = 180°)
Understanding the relationships between parallel lines and transversals is essential in geometry. These concepts appear everywhere from basic proofs to complex construction problems!
Answer
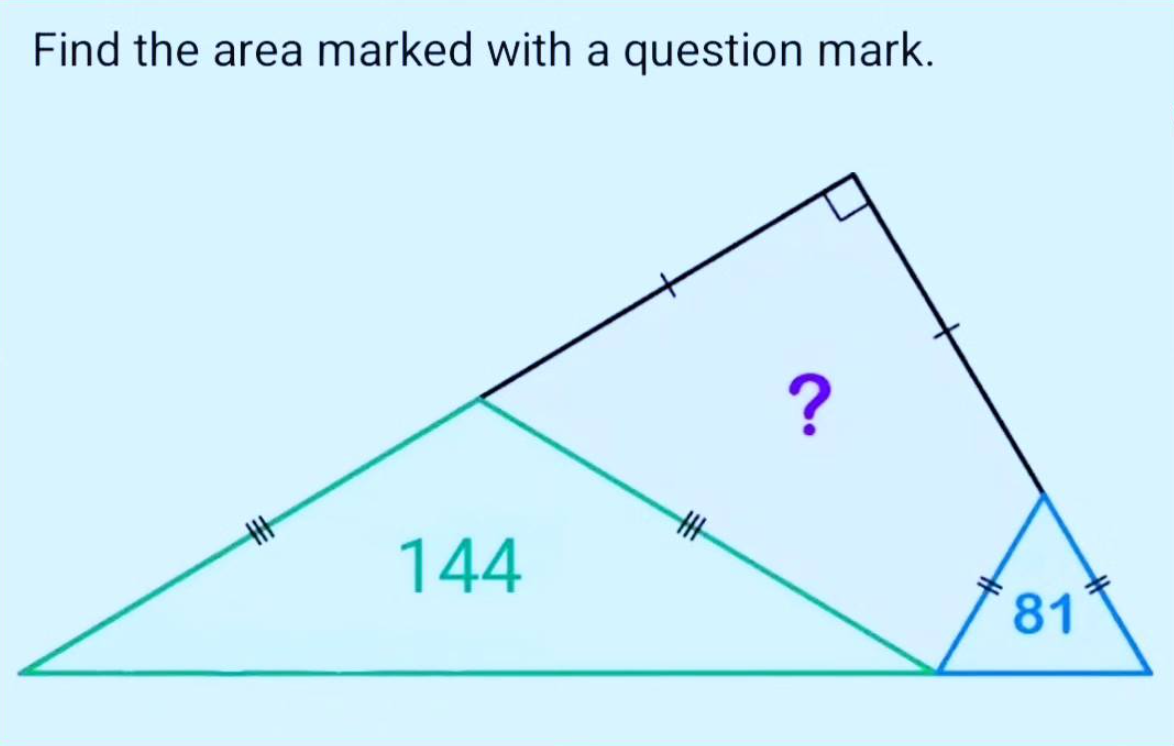
Finding the Area of the Quadrilateral: A Step-by-Step Explanation
Looking at the diagram, we have three shapes that share sides:
- A green/cyan triangle (bottom left) with area = 144
- A blue triangle (bottom right) with area = 81
- A black/dark quadrilateral (top) with area = ?
The most important clues are the tick marks on the sides. These tell us which sides are equal in length!
Step 1: Understanding the Tick Marks
The tick marks reveal:
- The green triangle has two equal sides (isosceles)
- The blue triangle has two equal sides (isosceles)
- The black quadrilateral has two equal sides AND a right angle at the top
Key insight: The black shape is actually a right isosceles triangle! It has two equal legs and a 90° angle between them.
Step 2: Naming Our Unknown
Let's call the hypotenuse of the black triangle s. This is the slanted side it shares with the green triangle.
Since the black triangle is right-isosceles:
- Each leg has length: s/√2 (this comes from the Pythagorean theorem in a 45-45-90 triangle)
- The angles at the base are both 45°
Step 3: Finding the Area of the Black Triangle
For a right triangle:
Area = (1/2) × base × height
Since both legs equal s/√2:
X = (1/2) × (s/√2) × (s/√2) = (1/2) × (s²/2) = s²/4
Step 4: Finding the Area of the Green Triangle
The green triangle has:
- Two sides of length s (from the tick marks)
- The angle between them is 45° (the base angle of the black right-isosceles triangle)
Using the formula for triangle area with two sides and included angle:
Area = (1/2) × side₁ × side₂ × sin(angle)
A_green = (1/2) × s × s × sin(45°) = (s²/2) × (√2/2) = (s²√2)/4 = 144
Step 5: Finding the Area of the Blue Triangle
The blue triangle has:
- Two sides of length s/√2 (same as the black triangle's legs)
- The angle between them is 45°
A_blue = (1/2) × (s/√2) × (s/√2) × sin(45°) = (s²/4) × (√2/2) = (s²√2)/8 = 81
Step 6: The Beautiful Relationship
Now let's multiply the green and blue areas:
A_green × A_blue = (s²√2)/4 × (s²√2)/8
= (s⁴ × 2)/32
= s⁴/16
But notice that:
s⁴/16 = (s²/4)² = X²
This means:
144 × 81 = X²
Step 7: Solving for XX² = 144 × 81
X² = 11,664
X = √11,664 = 108
The Answer
The area of the black quadrilateral is 108 square units.
Why This Works: The Big Picture
This problem demonstrates a beautiful geometric relationship: when you have a right isosceles triangle connected to two other isosceles triangles in this specific way, the area of the middle triangle is the geometric mean of the other two areas.
In other words:
X = √(A_green × A_blue)
This relationship exists because all three shapes share proportional dimensions based on the same length s, and the 45° angles create a perfect mathematical harmony between them.
Try It Yourself!
Can you see why this relationship holds? The key is recognizing that:
- All three areas are proportional to s²
- The specific angles (45°) create perfect ratios
- Multiplying the green and blue areas gives you the square of the black area
This is a wonderful example of how geometric constraints can create elegant mathematical relationships!



Comments ()