Did it work?

Did my picture of two hamsters dressed up as sushi for Halloween get you to click on the link? If so, YAY!!! Now let's do some math! (I'll put more cute pictures at the end of the post to reward you)
We've been attending weekend math events with the University of Texas Sunday Morning Math Group. This last weekend, the theme was every nerd's favorite topic, PRIME NUMBERS! YES, I know, right? Does it get any better than discussing the mysteries of prime numbers!?!?!
Below I'll attach the worksheets from the weekend but I'm putting the first problem into game form below!
🔢 Prime Numbers Challenge
Click all the prime numbers! (Numbers with exactly two divisors: 1 and itself)
Too easy? Feel free to step up your GAME with this version to 500!
Question 2:
Is 51 a prime number? Explain why or why not.
Answer:
No, 51 is not a prime number. A prime number must have exactly two divisors: 1 and itself. However, 51 can be divided evenly by 1, 3, 17, and 51. Since 51 = 3 × 17, it has more than two divisors, making it a composite number, not a prime.
Question 3:
Why is 2 the only even prime number?
Answer:
2 is the only even prime number because it's the only even number that has exactly two divisors (1 and 2). All other even numbers (4, 6, 8, 10, etc.) are divisible by 2, which means they have at least three divisors: 1, 2, and themselves. Since they have more than two divisors, they cannot be prime. Therefore, 2 is unique as the only even prime number.
Question 4:
Is 1 prime? Why or why not?
Answer:
No, 1 is not a prime number. By definition, a prime number must have exactly two divisors: 1 and itself. However, the number 1 only has one divisor (itself). Because 1 doesn't meet the requirement of having exactly two distinct divisors, it is neither prime nor composite—it's considered a special case or unit in number theory.
Question 5 (Advanced):
Prove by contradiction that there are infinitely many primes.
Answer (Euclid's Proof):
Assume, for the sake of contradiction, that there are only finitely many primes. Let's call them p₁, p₂, p₃, ..., pₙ, where pₙ is the largest prime.
Now consider the number N = (p₁ × p₂ × p₃ × ... × pₙ) + 1
This number N is formed by multiplying all the primes together and adding 1.
When we divide N by any of our primes (p₁, p₂, p₃, ..., pₙ), we always get a remainder of 1. This means N is not divisible by any of the primes in our list.
Therefore, either:
- N itself is prime (and it's larger than pₙ, contradicting our assumption that pₙ was the largest prime), OR
- N is divisible by some other prime that's not in our list (also contradicting our assumption that we had all the primes)
Either way, we've reached a contradiction. Therefore, our initial assumption must be false, and there must be infinitely many primes.
Question 6:
A Mersenne prime is a prime of the form 2ⁿ - 1.
Answer:
We'll prove this by contrapositive: If n is not prime (i.e., n is composite), then 2ⁿ - 1 is not prime.
Suppose n is composite, so n = ab where 1 < a, b < n.
Using the polynomial factorization hint: xⁿ - 1 = (xᵃ - 1)(xᵃ⁽ᵇ⁻¹⁾ + xᵃ⁽ᵇ⁻²⁾ + ... + xᵃ + 1)
Substituting x = 2 and n = ab:
2ⁿ - 1 = 2ᵃᵇ - 1 = (2ᵃ - 1)(2ᵃ⁽ᵇ⁻¹⁾ + 2ᵃ⁽ᵇ⁻²⁾ + ... + 2ᵃ + 1)
Since a > 1, we have 2ᵃ - 1 > 1.
Since b > 1, the second factor is also greater than 1.
Therefore, 2ⁿ - 1 has at least two factors greater than 1, making it composite (not prime).
By contrapositive, if 2ⁿ - 1 is prime, then n must be prime.
(b) Does the reverse always hold? That is, if n is prime, must 2ⁿ - 1 also be prime?
Answer:
No, the reverse does not always hold. Even when n is prime, 2ⁿ - 1 may or may not be prime.
Counterexample:
Let n = 11, which is prime.
2¹¹ - 1 = 2048 - 1 = 2047
However, 2047 = 23 × 89, so 2047 is composite, not prime.
Other examples:
- n = 2: 2² - 1 = 3 (prime) ✓
- n = 3: 2³ - 1 = 7 (prime) ✓
- n = 5: 2⁵ - 1 = 31 (prime) ✓
- n = 7: 2⁷ - 1 = 127 (prime) ✓
- n = 11: 2¹¹ - 1 = 2047 = 23 × 89 (composite) ✗
Therefore, while n being prime is a necessary condition for 2ⁿ - 1 to be prime, it is not a sufficient condition. Not all values of 2ⁿ - 1 are prime when n is prime—these special primes (when they do occur) are called Mersenne primes.
Question 7: Every even integer greater than 2 can be expressed as the sum of two primes. (a) Verify this statement for all even numbers from 4 to 20. Write each even number as a sum of two primes.
Answer:
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7 (or 5 + 5)
- 12 = 5 + 7
- 14 = 3 + 11 (or 7 + 7)
- 16 = 3 + 13 (or 5 + 11)
- 18 = 5 + 13 (or 7 + 11)
- 20 = 3 + 17 (or 7 + 13)
✓ All even numbers from 4 to 20 can indeed be expressed as the sum of two primes.
(b) Every even integer greater than 2 can be expressed as the sum of two primes.: Prove this statement!
Historical Context and Challenges:
This is Goldbach's Conjecture, proposed by German mathematician Christian Goldbach in a 1742 letter to Leonhard Euler. It is one of the oldest and most famous unsolved problems in mathematics—it has remained unproven for over 280 years.
What We Know:
✓ Verified by computation: The conjecture has been verified for all even numbers up to 4 × 10¹⁸ (as of 2024) using computers, with no counterexamples found.
✓ Weak Goldbach's Conjecture: In 2013, Harald Helfgott proved the "weak" or "ternary" version: every odd number greater than 5 can be expressed as the sum of three primes. This was a major breakthrough but doesn't solve the strong conjecture.
✓ Near-miss results: In 1966, Chen Jingrun proved that every sufficiently large even number can be expressed as the sum of either two primes OR a prime and a semiprime (product of two primes). This is called Chen's Theorem.
Why It's So Difficult:
- Distribution of Primes: While primes become less frequent among larger numbers, we don't have a formula that predicts exactly where they appear. This makes it hard to guarantee that two primes will always sum to any given even number.
- No Unifying Framework: Unlike Fermat's Last Theorem (solved in 1995), Goldbach's Conjecture doesn't fit neatly into existing mathematical frameworks. There's no obvious pathway to a proof using current techniques.
- Simple Statement, Complex Behavior: The conjecture is easy to state but involves the subtle interplay between addition (a simple operation) and primality (a multiplicative property), which are fundamentally different aspects of number theory.
- Probabilistic vs. Deterministic: Probabilistically, the conjecture seems obvious—there are "enough" primes that pairs should exist. However, proving this deterministically for ALL even numbers requires understanding deep patterns in prime distribution.
Current Status:
Despite being tested extensively and believed to be true by virtually all mathematicians, Goldbach's Conjecture remains unproven. It stands alongside the Riemann Hypothesis as one of the most important unsolved problems in mathematics. Many consider it more difficult than Fermat's Last Theorem was, as there's currently no clear mathematical machinery that could lead to a proof.
The Clay Mathematics Institute has not included it among their Millennium Prize Problems, but solving it would undoubtedly be considered one of the greatest achievements in number theory.
Prime factorization means breaking down a number into a product of prime numbers. Every whole number greater than 1 can be written as a unique product of prime numbers; this is called the Fundamental Theorem of Arithmetic.
Express these numbers as products of prime powers (like 2² × 3):
48
48 = 2⁴ × 3
90
90 = 2 × 3² × 5
150
150 = 2 × 3 × 5²
200
200 = 2³ × 5²
🔢 Prime Factorization Practice
Enter the prime factors separated by spaces.
Example: For 20, enter: 2 2 5
Below are the full worksheets from the meetup! Bonus points to anyone who can solve 7B!




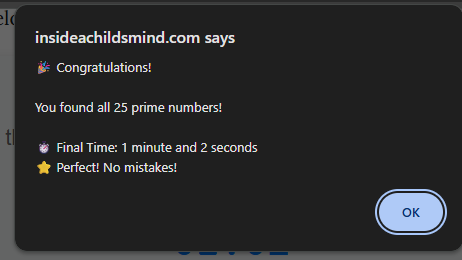
Edit: BOOM, the bar has been set on the prime numbers challenge!


Comments ()